PLAN du COURS :
Objectifs : Nous allons travailler dans le système ZFC
(Zermelo-Fraenkel with Choice). Après avoir montré rapidement la nécessite d'une
axiomatisation de la théorie des ensembles nous allons, dans un premier temps,
lister les axiomes de cette théorie, puis montrer qu'ils permettent de
définir proprement la notion fondamentale d'ordinal. Nous pourrons alors
constater l'existence d'un ordinal particulier, 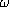 , qui vérifie l'axiomatique de Peano, et que nous appellerons provisoirement
N. Nous profiterons de l'occasion
offerte pour définir les opérations sur les ordinaux, et surtout pour construire
les ensembles de nombres usuels (N, Z, Q, R, C). Un chapitre tout entier sera
consacré à la construction de R
et aux principales propriétés de R.
, qui vérifie l'axiomatique de Peano, et que nous appellerons provisoirement
N. Nous profiterons de l'occasion
offerte pour définir les opérations sur les ordinaux, et surtout pour construire
les ensembles de nombres usuels (N, Z, Q, R, C). Un chapitre tout entier sera
consacré à la construction de R
et aux principales propriétés de R.
Nous
irons en fait le plus loin possible, c'est-à-dire jusqu'à la définition et aux
premières propriétés des cardinaux, sans utiliser l'axiome du choix. Nous
examinerons ensuite les diverses variantes de l'axiome du choix et leurs
conséquences classiques avant de revenir, mieux armés, à l'étude plus particulière
de l'arithmétique élémentaire sur les cardinaux transfinis.
Plan du cours :
Introduction : Un bref historique
Comment les «mauvaises séries» et la «fausse équation de la chaleur»
de Fourier conduisirent Georg Cantor à se pencher sur le problème des ensembles
exceptionnels
La crise des fondements
Les premières tentatives
d'axiomatisation
Les problèmes actuels
Chap0 : Ensembles bien ordonnés
Ensembles ordonnés
Ensembles bien
ordonnés
Axiomatique de Peano standard
Une autre axiomatique
équivalente
Autres exemples d'ensembles bien ordonnés / Ensembles bien
ordonnables
Chap1 : Quelques préliminaires de logique
élémentaire
Symboles de base
Expressions et
formules
Quelques simplifications usuelles
Variables liées, variables
libres
Déduction formelle
Chap2 : Les axiomes
Chap3 : Relations, fonctions, bons
ordres
Chap4 : Ordinaux
Définitions
Propriétés élémentaires des ordinaux
Chap5 : Construction des ensembles de nombres
usuels
L'ordinal 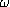 / Construction de N
/ Construction de N
L'addition dans N
La
multiplication dans N
Construction de Z
Construction de Q
L'axiome de l'ensemble des parties
Construction de
R
Construction de C
Chap6 : L'axiome du choix / Prolongements
ultérieurs
Chap7 : Le corps des nombres
réels
Inventaire des propriétés de Q
Suites convergentes / Suites de
Cauchy
L'axiome de l'ensemble des parties
Construction de R
Caractérisation de
R
Quelques propriétés de R
Parties remarquables de R
Chap8 : Compléments sur l'arithmétique des
ordinaux
Le théorème de récursion
Le principe de
récurrence transfinie
Addition des ordinaux
Multiplication des
ordinaux
Exponentiation des ordinaux
Chap9 : Topologie sur les ordinaux / L'ordinal oméga un / Les
ordinaux oméga alpha
Topologie sur les ordinaux
La hiérarchie des bons
ordres sur 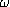 / L'ordinal oméga un
/ L'ordinal oméga un
Généralisation
Chap10 : Cardinaux
Le théorème de
Cantor-Bernstein
Définition de la cardinalité
Notion de cardinal
La
hiérarchie des cardinaux transfinis
Les problèmes
Chap11 : Différentes formes de l'axiome du choix / Applications
diverses
L'axiome du choix lui-même
Un lemme de théorie des
ensembles
Le principe de maximalité de Hausdorff
Le lemme de
Zorn
Quelques applications du lemme de Zorn
Le théorème de Zermelo
Une
application du théorème de Zermelo
Retour à la case
départ
Complément
Un peu de philosophie
Chap12 : Influence de l'axiome du choix sur la hiérarchie des
cardinaux transfinis
Un théorème de Cantor
La hiérarchie des cardinaux
transfinis, deuxième épisode
Une curiosité
Chap13 : Un peu d'arithmétique élémentaire sur les cardinaux
transfinis
Rappels
Opérations sur les cardinaux
Fonctions et
cardinaux
Exponentiation des cardinaux
Notion de cofinalité / Cardinaux
réguliers / Cardinaux inaccessibles
Annexe I : L'axiomatique de Zermelo-Fraenkel with Choice
(ZFC)
Annexe II : L'Hôtel de Hilbert
Annexe III : Le principe des tiroirs et des chemises
Annexe IV : Bibliographie sommaire
Lire l'Introduction : Un bref Historique
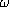 , qui vérifie l'axiomatique de Peano, et que nous appellerons provisoirement
N. Nous profiterons de l'occasion
offerte pour définir les opérations sur les ordinaux, et surtout pour construire
les ensembles de nombres usuels (N, Z, Q, R, C). Un chapitre tout entier sera
consacré à la construction de R
et aux principales propriétés de R.
, qui vérifie l'axiomatique de Peano, et que nous appellerons provisoirement
N. Nous profiterons de l'occasion
offerte pour définir les opérations sur les ordinaux, et surtout pour construire
les ensembles de nombres usuels (N, Z, Q, R, C). Un chapitre tout entier sera
consacré à la construction de R
et aux principales propriétés de R.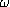 / Construction de N
/ Construction de N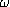 / L'ordinal oméga un
/ L'ordinal oméga un