Introduction : Un bref historique

Les citations proposées dans ce chapitre sont empruntées à un ouvrage de Ian Stewart qui s'intitule «Les mathématiques», publié chez Belin. (C'est le même qui a écrit «Galois Theory», cet ouvrage remarquable, si cher aux agrégatifs de tout poil).

Chose curieuse, le formalisme mathématique tel que nous le connaissons aujourd'hui est une science relativement jeune. Sans exagérer on peut situer la préhistoire au début des années 1870, lorsque Monsieur Georg Cantor décida, pour des raisons sur lesquelles nous allons revenir, de s'intéresser au problème des ensembles exceptionnels. S'ensuivit une période de flottement durant laquelle moults mathématiciens éminents eurent pour mission de «digérer» les idées géniales du «maître». C'est aussi pensant cette période que l'on s'aperçut que ce n'était pas aussi évident que cela paraissait de faire dériver l'ensemble des mathématiques d'un nombre fini de postulats. C'est seulement au début du vingtième siècle que l'on put assister aux premières tentatives d'axiomatisation de la théorie des ensembles. Le système ZFC tel que nous le pratiquons aujourd'hui a vu le jour en 1926. D'autres systèmes ont suivi mais ils ont tous la même consistance. (Si ZFC est non contradictoire il en est de même des autres systèmes et réciproquement). Enfin, après la remise en cause par Gödel, puis Cohen, de l'«immuabilité» de la science mathématique il a fallu attendre les années 1970 pour que le formalisme de la théorie des ensembles soit accepté comme une branche des mathématiques à part entière, et non plus comme un «délire» de logiciens en mal de raisonnements hypothético-déductifs.

I) La préhistoire : le problème des ensembles exceptionnels

Il est quelques aberrations dans l'histoire des mathématiques. En voici une, et pas des moindres. Rendez-vous compte, c'est un physiqueux qui est à l'origine de la théorie des ensembles. Honte à nous!

«...Tout a commencé avec les travaux de Joseph Fourier sur l'équation de la chaleur. Ayant représenté les phénomènes par une équation, dite équation de la chaleur, il s'efforça ensuite de la résoudre. Au cours de ce travail il s'aperçut que tout serait merveilleux s'il réussissait à représenter n'importe quelle fonction par une série de sinus et de cosinus. Il mit au point une longue démonstration, établit une formule donnant les coefficients de la série et s'en servit dans son ouvrage Théorie analytique de la chaleur pour résoudre une grande variété de problèmes d'échanges thermiques.»

Well. Nul ne met en doute, de nos jours, l'importance des séries de Fourier, aussi bien en électronique que dans certaines branches de l'analyse. Mais quand même, à la lecture de la citation suivante vous allez vous marrer.

«...Je dois ajouter enfin que les raisons données par Fourier de son développement des fonctions en séries de sinus et de cosinus étaient complètement absurdes. Les démonstrations sont approximatives, confuses et fausses. Le style de démonstration de Fourier ne peut conduire qu'à de mauvaises mathématiques. Les réponses ne sont pas toujours exactes, et les arguments «physiques» de Fourier ne sont que des prétextes pour justifier ce qu'il pensait être exact, et qui s'est souvent révélé faux. Tout ce domaine est beaucoup plus subtil que Fourier ne l'imaginait, et il a fallu près d'un siècle de travail pour s'en faire une idée correcte. L'une des conséquences de son travail fut l'oeuvre de Cantor sur la théorie des ensembles, et nombre des applications actuelles de l'analyse de Fourier seraient impossibles si l'on n'avait pas d'abord acquis une compréhension correcte de ce qui se passe, mathématiquement parlant.»

Quel rapport avec le sujet qui nous préoccupe? Nous y venons. En plein fiasco de l'époque (les seventies, mais du siècle dernier), les mathématiciens cherchent à résoudre le problème suivant, qu'on appelle à juste titre le problème des ensembles exceptionnels :

Soient f et g 2 fonctions développables en série de Fourier sur :

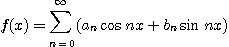
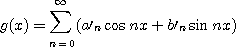
On sait que, si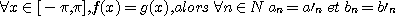

(C'est clair).

Question : Qu'en est-il si f(x)=g(x) partout sauf sur un ensemble «exceptionnel»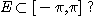

Evidemment si E est fini ça marche encore, et dans le but d'aller plus loin Cantor a été amené à étudier la structure des ensembles infinis, par exemple inclus dans [0,1].

II) Premiers balbutiements : les grandes découvertes de Cantor

1) Les différents infinis

Constatant que le problème des ensembles exceptionnels a encore une réponse positive pour certains sous-ensembles infinis particulièrement simples, Cantor décide de créer une véritable théorie des ensembles infinis. Il prend comme définition ce que ses prédécesseurs ont toujours considéré comme une sorte d'aberration de la nature.

Définition 1 (Cantor) : Un ensemble E est infini ssi il existe une bijection de E sur une partie stricte de lui-même.

Exemple : L'application de N dans N-{0} qui à tout nombre associe son successeur.

Définition 2 : 2 ensembles E et F sont équipotents, ou possèdent le même cardinal, ssi il existe une bijection de E sur F.

En ce sens, le plus petit des ensembles infinis est bien sûr l'ensemble N. Son cardinal est noté 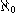(aleph zéro), c'est le plus petit des cardinaux infinis.

Définition 3 : E est dénombrable ssi 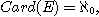i.e. ssi il existe une bijection de N sur E.

Cantor démontre sans difficulté que Z, D et Q sont dénombrables. Dans la foulée il pense qu'il en est peut-être de même de R, auquel cas le symbole «aleph zéro» ne serait qu'une nouvelle façon de noter l'infini. Il n'en est rien, Cantor démontre lui-même que R n'est pas dénombrable, nous en verrons plusieurs démonstrations dans ce cours, dont celle de Cantor au Chap 7. C'est donc qu'il existe au moins deux sortes d'infinis : le dénombrable et le continu. Plus tard, Cantor démontre que si E est un ensemble, alors il n'existe pas de bijection de E sur , l'ensemble des parties de E. 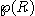C'est donc qu'en un certain sens R est strictement plus petit que ,qui lui-même est strictement plus petit que 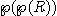,et ainsi de suite. Il existe donc une infinité de sortes d'infinis.

2) Les dérivées de Cantor

Toujours dans le but de résoudre le problème des ensembles exceptionnels, Cantor décide d'étudier les compacts dénombrables.

E désignant un espace topologique, Cantor appelle ensemble dérivé de E l'ensemble 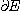de tous les points d'accumulation de E. L'ensemble 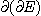est noté 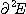et ainsi de suite.

Par exemple,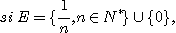alors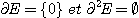

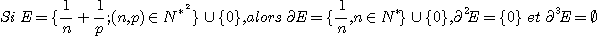
Il serait raisonnable de penser que, si on note 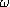le cardinal de l'ensemble N, le phénomène de dérivation «sature» après au maximum 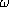opérations. En fait,Cantor démontre que si on note

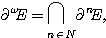
alors il existe certains espaces E, plus compliqués, pour lesquels 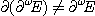et ainsi de suite. C'est donc qu'il existe quelque part des «nombres» 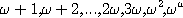etc.

3) Les ordinaux

Cantor invente les ordinaux pour classifier les compacts dénombrables. (On dira que le compact K est de classe 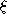si 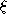est le plus petit ordinal tel que ).

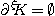Mais Cantor ne se pose pas de questions «philosophiques» sur la validité de ce qu'il affirme. Par exemple, l'existence d'un bon ordre sur R est pour lui une trivialité : je choisis un élément au hasard dans R, je l'appelle 0, je choisis un élément au hasard dans R-{0},je l'appelle 1 etc., et pour peu que j'aie suffisamment de patience je finirai bien par «manger» tous les réels.

III) Premières tentatives d'axiomatisation : la crise des fondements

On entre alors dans une ère de formalisation (Frege, Russel etc.).

Le premier écueil rencontré est celui du paradoxe de Russel : le barbier du village rase tous les hommes qui ne se rasent pas eux-mêmes. Question : le barbier se rase-t-il lui-même? Réponse : s'il se rase lui-même, il rase quelqu'un qui se rasait déjà lui-même, contradiction. S'il ne se rase pas il omet de raser quelqu'un qui ne se rase pas lui-même, contradiction également.

On verra que ce paradoxe revient à considérer l'ensemble de tous les ensembles qui ne s'appartiennent pas à eux-mêmes. (Question : cet ensemble s'appartient-il à lui-même?).

Deuxième écueil sur la route : l'ensemble de tous les cardinaux. Cet ensemble a un cardinal, qui est nécessairement strictement plus grand que tous les cardinaux, y compris lui-même. Problème.

On a finalement résolu le problème en restreignant la notion même d'ensemble. On s'est décidé à admettre petit à petit, mais cela a pris un certain temps, qu'il existe des propriétés «non collectivisantes», c'est-à-dire qui ne permettent pas de définir un ensemble en compréhension (exemples : être un ensemble, être un cardinal, ne pas s'appartenir à soi-même etc.).Cela revient à dire qu'il existe des «objets» qui sont trop gros pour être des ensembles : la collection de tous les ensembles, de tous les ordinaux, de tous les cardinaux, de tous les corps isomorphes à R etc. Ce palliatif ne satisfait personne, certes, mais au moins il a permis d'énoncer une axiomatique cohérente, du moins apparemment.

Avant de dire un mot de l'hypothèse du continu je voudrais citer une dernière fois Stewart, ça vaut son pesant de cacahuètes de lire ce qu'il pense des détracteurs de Cantor...

«...Les mathématiciens ont été très partagés sur l'importance des idées de Cantor. Pendant une dizaine d'années Leopold Kronecker les a attaquées publiquement et violemment, au point que Cantor finit par être victime d'une dépression nerveuse. Kronecker avait une vision plutôt restrictive des mathématiques. «Dieu créa les nombres entiers, disait-il, tout le reste est l'oeuvre de l'homme.» L'idée qu'il aurait pu approuver les idées de Cantor était naïve. Poincaré disait que les générations futures considéreront ces théories comme une maladie dont on a heureusement réchappé. Hermann Weyl reconnaissait que l'infinité des infinis de Cantor était du brouillard par dessus le brouillard. Cependant Adolf Hurwitz et Hadamard découvrirent d'importantes applications de la théorie des ensembles à l'analyse et en firent mention dans de prestigieux congrès internationaux. Hilbert, qui était le premier mathématicien de son temps, déclara en 1926 : «Personne ne pourra plus nous chasser du paradis que Cantor a créé», et il fit l'éloge de ses idées : «Le produit le plus étonnant jamais engendré par la pensée mathématique.» Comme pour d'autres idées à l'originalité percutante, seuls purent les apprécier ceux qui acceptèrent de faire un effort pour les comprendre et en tirer parti dans leurs propres travaux. Les commentateurs marginaux ou portés au dénigrement ont laissé le sentiment de leur propre importance aveugler leur goût et leur imagination. De nos jours,l es fruits de l'oeuvre de Cantor sont à la base de toutes les mathématiques.»

Remarque personnelle : J'espère que le lecteur aura, tout comme moi, été sensible à l'humour particulièrement acéré de l'auteur. Je dois avouer que, ne portant guère dans mon coeur les mathématiqueux appliqués, empêcheurs de cogiter en rond, finitistes, nihilistes et autres Saint-Thomas de la mathématique moderne, j'en ai eu pour mon argent à la lecture de ces quelques lignes.

IV) Les problèmes actuels

Suite aux travaux de Cantor il a fallu une trentaine d'années pour qu'on commence à envisager que peut-être l'existence d'un bon ordre sur tout ensemble ne pouvait-elle se déduire du reste des axiomes de la théorie. On sait aujourd'hui que c'est vrai, mais ce n'est qu'en 1905 que Zermelo décide de le poser en postulat. Ce postulat, connu sous le nom de «théorème de Zermelo», est en fait équivalent à l'axiome du choix.

Il restait encore un problème que Cantor n'avait pas réussi à résoudre, et qu'il avait alors ramené à une conjecture baptisée «hypothèse du continu». Il s'agissait de savoir s'il existait ou non des ensembles de cardinal strictement compris entre le dénombrable et le continu. En 1933 Gödel démontre qu'il est impossible de démontrer que c'est faux, et en 1962 Cohen démontre qu'il est impossible de démontrer que c'est vrai. l s'agit d'une propriété indécidable. Tout dépend de votre version de la théorie des ensembles. C'est comme le problème des parallèles d'Euclide : il est impossible de le déduire du reste de la théorie... Et le pire c'est que c'est un phénomène général. D'après le premier théorème d'incomplétude de Gödel toute théorie contenant au moins l'arithmétique classique conduit un jour ou l'autre à une propriété indécidable.

C'est ainsi, il faut s'y faire...

Les chapitres suivants sont au format pdf